Questions

What is Diffusion Model?
How diffusion models work?
What can diffusion models do?

近期diffusion model在很多地方都被应用，如Tsinghua - Liu Yebin团队CVPR paper DiffuStereo，在此对扩散模型做一个简单的阅读，提出三个问题看在文档结尾能否给自已一些答案

Surveys & Blogs

Diffusion Models in Vision: A Survey
Understanding Diffusion Models: A Unified Perspective, by Calvin Luo, Google Brain
What are Diffusion Models? - Lil’s Blog
由浅入深了解Diffusion Model - ewrfcas’s Zhihu Article

DDPM

| Denoising Diffusion Probabilistic Models

Overview

如 [1] [2] 等文章中阐述，diffusion model实际是一种生成模型。Model主要包含两个part，添加T轮的噪声部分 (Forward Pass) 以及对噪声图进行denoise的部分 (Reverse Pass)。

DDPM

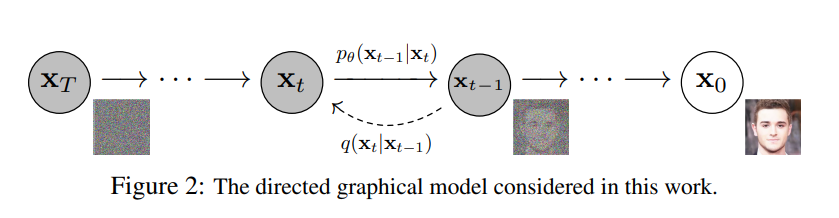
Forward Pass (Diffusion Pass)

Forward Pass即对图片$x_0 \sim q(x)$逐次添加噪声的过程，并最终呈现为完全的噪声分布。在添加噪声的过程中，每一个时刻$t$只与先前时刻$t-1$以及对应的Gaussian噪声有关。其中，$x_1, x_2, … x_t$均为与原图像同维度的latent code。即有

$$
q(x_t|x_{t-1}):=\mathcal{N}(x_t;\sqrt{1-\beta_t}x_{t-1}, \beta_tI)
$$

其中$\beta \in (0,1)$为扩散率，实际中随着$t$的增大而增大。
整个过程可以被看成不断添加噪声的Markov过程，对于任意时刻$t$则有

$$
q(x_{1:t}|x_0):=\Pi_{i=1}^tq(x_i|x_{i-1})
$$

另外在[1]中也证明了，对于Gaussian分布，对于任意时刻$t$，若$\alpha_i:=1-\beta_i, \bar{\alpha}_i:= \Pi _{s=1}^i\alpha_s$有

$$
q(x_t|x_0)=\mathcal{N}(x_t;\sqrt{\bar{\alpha}_t}x_0,(1-\bar{\alpha}_t)I)
$$

这可以让我们通过$x_0,\beta$来快速获取时间$t$下的$x_t$，实际上即有

$$
x_t = \sqrt{\bar{\alpha}_t}x_0+\sqrt{1-\bar{\alpha}_t}\epsilon
$$

Reverse Pass

与Forward Pass相反，在Reverse Pass中我们希望找出一个分布$p_\theta(x_{0:t})$，也由一个高斯核转移的Markov链来定义：

$$
p_\theta(x_{t-1}|x_t):=\mathcal{N}(x_{t-1}; \mu_\theta(x_t,t), \sum_\theta(x_t,t))
$$

其中$\theta$为模型参数。对于任意时刻$t$则有

$$
p_\theta(x_{0:t}):=p(x_t)\Pi_{i=1}^tp_\theta(x_{t-1}|x_t)
$$

虽然无法得到分布$q(x_{t-1}|x_t)$，但在我们知道$x_0$的情况下，可以通过贝叶斯公式得到

$$
\begin{aligned}
q(x_{t-1}|x_t, x_0)&=q(x_t|x_{t-1},x_0)\frac{q(x_{t-1}|x_0)}{q(x_t|x_0)}\
&= … \
&=\mathcal{N}(x_{t-1};\tilde{\mu}(x_t,x_0),\tilde{\beta}_tI)
\end{aligned}
$$

利用上述式子可以将Reverse Pass转变为更易求解的Forward Pass，而其中的$\tilde\mu$可以由预测的Gaussian分布和$x_t$得到，在DDPM中有$\sum_\theta(x_t,t)=\tilde\beta_t$，即可以表征当前时刻的分布。对于网络则需要学习出时刻$t$下的高斯噪声分布。

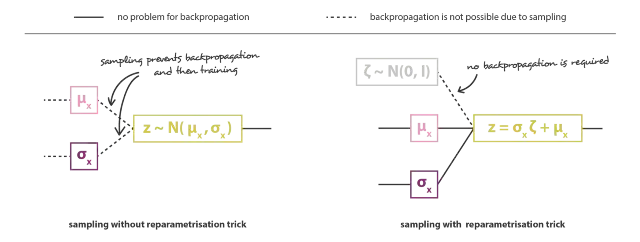
Reparameterization

和VAE类似，我们希望整个过程是可导的来完成训练的过程，而从一个高斯分布中进行采样这个过程是不可导的，而在Diffusion Model中每一步都充满了高斯分布的影响。因此和VAE一样，在Diffusion Models中也采用了重参数的技巧来使得采样过程变得可导。

$$
z=\mu_\theta+\sigma_\theta \cdot \epsilon, \epsilon \in \mathcal{N}(0,I)
$$

对于一个高斯分布$z$来说，他可以被描述成上式的形式，利用上式的写法，其仍然是满足以均值为$\mu_\theta$、方差为$\sigma_\theta^2$的高斯分布，而随机性被转移到了$\epsilon$上。

Reparameterization

Training

与VAE类似，在[1]中推导出其训练损失即为组合的KL散度和熵，在[1][2]等中都有较为详细的推导。
Training

而$L_0$则认为是一个离散化的过程，构建一个离散化的分段积分累乘。即在Sampling过程中$t==1$获取生成图片时不需要在这一步继续添加噪声求解。实际上，网络学习的就是每一个时刻和下一个时刻

Conclusion

本质上，DDPM就是通过网络来学习到时刻$t$的噪声，并利用推导的公式来进行$t-1$时刻的生成，并不断重复此过程来获取最终生成的图片。而训练的时候，输入为$x_0$和噪声$\epsilon$的线性组合即$x_t$和时刻$t$，并通过对应的Loss进行约束训练。

但图像的质量往往取决于采样频率$T$的多少，而频率高了之后带来的问题是采样过程、训练过程十分漫长。在DDIM[4]中对这个问题进行了研究，并对此进行了加速。[4]中对$q(x_{t-1}|x_t, x_0)$进行推导分析，实际可以利用起始点和终点直接算出$q(x_{x}|x_k, x_0)$，即可以不像DDPM一样逐次采样，从而减少采样次数。

SR3

| Image Super-Resolution via Iterative Refinement

文章[5]则是利用了Diffusion来做超分的任务。

Conditional Reverse Pass

和DDPM、DDIM不同，超分是一项特定的任务，因此在reverse pass中需要加入条件约束。因此在SR3中提出，原先在reverse pass中只需要输入$(x_t, t)$，而在超分任务中需要将LR image插值到HR image大小后，concat作为网络的输入。

SR3

除此之外，上图中的$p(\gamma)$实际上是噪声率。在DDPM中通过不断扩散的方式进行添加噪声，将时刻$t$加入到网络的输入中。而在SR3中则取消了时刻的输入，而是直接改为将当前的噪声率$\gamma$embedding。而这个$\gamma$在训练过程中实际上是对间隔$[\bar{\alpha}_{t-1}, \bar{\alpha}_t]$的一个均匀采样，与DDPM直接取$\bar{\alpha}_t$不同。

Furthur Thoughts

利用SR3的思路，实际上对于Image2Image的任务，都可以通过类似这种形式简单粗暴地改写reverse pass。如对于deblur，也可以通过这种方法，将noise图片作为condition一起输入到网络中，作为reverse阶段的输入。

DSR - Deblur

| Deblurring via Stochastic Refinement

DSR

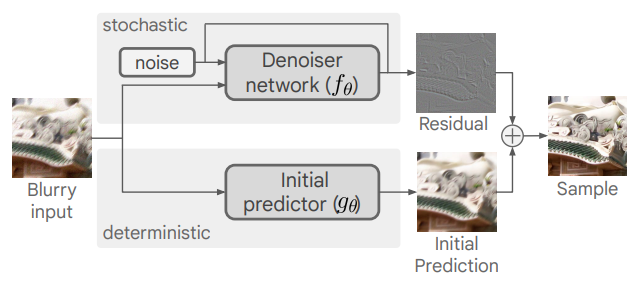
Split Branch

如上图的overview，在这篇CVPR的deblur文章中，对于模糊图片的处理采用了两个模块：一个是initial预测deblurred的模块，另一个则是使用diffusion来预测残差的模块。最终将两个output结合生成deblurred image。

Miscs

另外与DDPM等不同的是，DSR仍然采用的和SISR相似的策略，在patch上训练，在image上inference.而由于每一次的采样都具有随机性，为了让结果更为稳定，文章中采用多次重建取均值的方式来提升最终的效果。

Back to NCSN - Score-Based Modeling

| Generative Modeling by Estimating Gradients of the Data Distribution

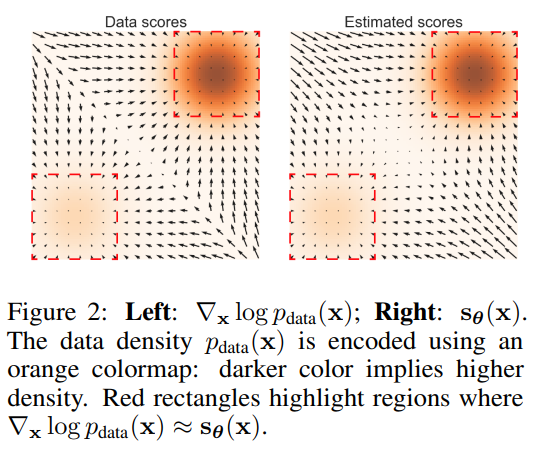
Scores

Score and Generation

实际上这一篇NCSN(Noise Coinditional Score Network, or Score-Based Modleing)[7]比DDPM更早将扩散模型作为生成模型来使用。在NCSN中，score实际上就是数据分布的梯度，利用这个score可以让我们从一个噪声基于Langevin Dynamics采样（实际上DDPM的采样也是类似这种形式），来生成最终的image。文章提出由于低密度区域的数据分布的score其实很难预测，这会导致很难或无法通过这些预测很差的score来生成最终的数据分布。因此NCSN提出，可以通过在数据中加入Gaussian噪声的方式，来扩大原先高密度的区域，这样能够使低密度区域相比与先前更容易预测score。由于添加了噪声会导致数据分布与原先不大一致，因此添加噪声的强弱等也属于一个tradeoff，需要让其不断增强对低密度区域的预测，但也要同时尽量保持希望的数据分布。

若$p_\theta(x)$为概率分布，实际上score即为$\nabla\log p_\theta(x)$，即概率的对数梯度。score的趋势即指向数据密度更高的方向，如上图所示。生成的过程即我们在空间中的点，每一个点通过Langevin Dynamics采样来不断逼近目标数据。即

$$
x_t\leftarrow x_{t-1}+\frac{\epsilon}{2}\nabla\log p_\theta(x_t)+\sqrt{\epsilon}z_t
$$

Sampling

实际上上述采样的过程即为分L步，期间每一步确定了noise level和步长，然后在这每一步中再进行T次的Langevin Dynamics采样。实际上在T=1的时候，和DDPM中的采样方式是一致的。

How to Get Scores

实际上估计score就是估计每一次添加的噪声（实际上score和噪声相比只差一个scale，基于添加的Gaussian噪声）。

在文章[8]（非常solid的一篇paper）中，将diffusion model与SDE的关系进行了更为详细的阐述，对连续形式的diffusion pass和reverse pass进行了构建说明，并将NCSN和DDPM进行了整合。实际上，NCSN要得到最终的一张纯噪声图，由于是在原图上直接进行的添加，因此需要非常大的噪声来掩盖原图的信息；而DDPM实际上是通过对原图进行比例控制来达到相同的目的。

DiffuStereo

| DiffuStereo: High Quality Human Reconstruction via Diffusion-based Stereo Using Sparse Cameras

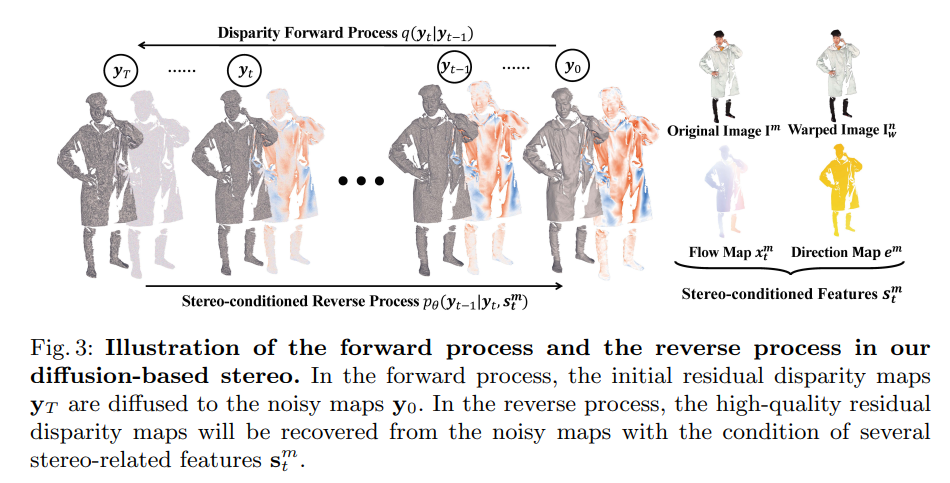
DiffuStereo

Diffusion in DiffuStereo

在DiffuStereo一文中，作者利用diffusion model来对disparity进行refine。其中diffusion model不是直接将disparity map进行refine，而是将其与gt的残差作为model的输入。

实际上，DiffuStereo中的diffusion和SR3类似，也是一种conditional diffusion。DiffuStereo中利用了origin image、warped image、flow map（利用init flow和当前时刻的residual计算）和direction map一起作为输入来当作diffusion model的condition。和DDPM等不同的是，DiffuStereo的采样过程中扩散率是线性增加的。另外，对于initial的输入，DiffuStereo还做了一个global feature，将其应用于diffusion model的各个时刻。

$$
L_t=\mathbb{E}_{y_0,\epsilon,t}[||f_\theta((1-\gamma_t)y_0+\gamma_t\epsilon,s,t)-y_0||^2]
$$

在Supp. Mat.中，diffusion model的训练损失是每一个时刻输出与$y_0$的$L_2$损失，见上式。和SR3类似，只是将模型直接预测噪声转成了预测残差值，即当前时刻的观测与噪声的线性组合。

Diffusion model在DiffuStereo中的作用就是改进flow map(disparity map)，它是一个独立的模块，理论上可以提供给所有的stereo来做refine。但原文并没有将这个module在别的stereo method进行实验，因此无法下结论是否这个模块在stereo method上都能够对结果有进一步提升，但是一个可以尝试的思路。

End of this Doc

What is Diffusion Model?

扩散模型实际上和GAN类似是一种生成模型，输入噪声图经过model得出需要的结果。

How diffusion models work?

扩散模型通过定义添加噪声的forward pass/diffusion pass和denoise的reverse pass以及相关的loss和数学推导来完成模型的训练，训练的model实际上是用于预测当前时刻/噪声率下的噪声，并以此不断迭代最终生成需要的image的过程。
和GAN相比，GAN需要训练生成器和判别器两个模型，整个过程相对于diffusion model只需要训练一个过程而言更复杂且不稳定。而在生成任务中diffusion model能够达到很好的效果。

What can diffusion models do?

In vision，扩散模型已经有研究人员们用于做图片生成、超分、去噪、甚至于检测(DiffusionDet)等一系列任务中。总体而言本质上需要我们定义好reverse的过程以及对应的condition，可以在对应的任务进行尝试。在多模态领域，diffusion model也有非常出色的表现。

Pros & Cons

如上述问题中所回答的，扩散模型可以高效的解决GAN等生成模型训练不稳定的问题，并且结构易于设计和实现。但同时，其依赖于高斯噪声假设来进行数学推理，可能会导致与真实场景的噪声不匹配。另外在inference过程中，由于需要经过多个采样步骤，和GAN相比其推理时间会更长。

What are the differences between diffusion models and recurrent U-Net?

从inference pass而言，diffusion model输入$(x_t,t[\gamma, or else, …])$，然后将输出不断的当成输入继续送入网络。而对于recurrent U-Net来说，也是将得到的结果不断在U-Net中循环计算。但不同的是，diffusion model还需要知道当前的时刻$t$或是噪声率$\gamma$等相关的参数，然后在当前步骤中进行下一个时刻的求解；而不断的重复U-Net仅仅是对输入时刻的数据进行相同的求解。正如DDIM中阐述的，diffusion model的本质可以看成是一个SDE的求解的离散化过程，而在单一的不断重复的U-Net中实际上并不能改变其求解方向。