Stereo Vision
Stereo Vision: A Brief Introduction
如何获取三维信息
从相机模型可以了解我们是如何将三维世界的物体映射到二维图片上的。
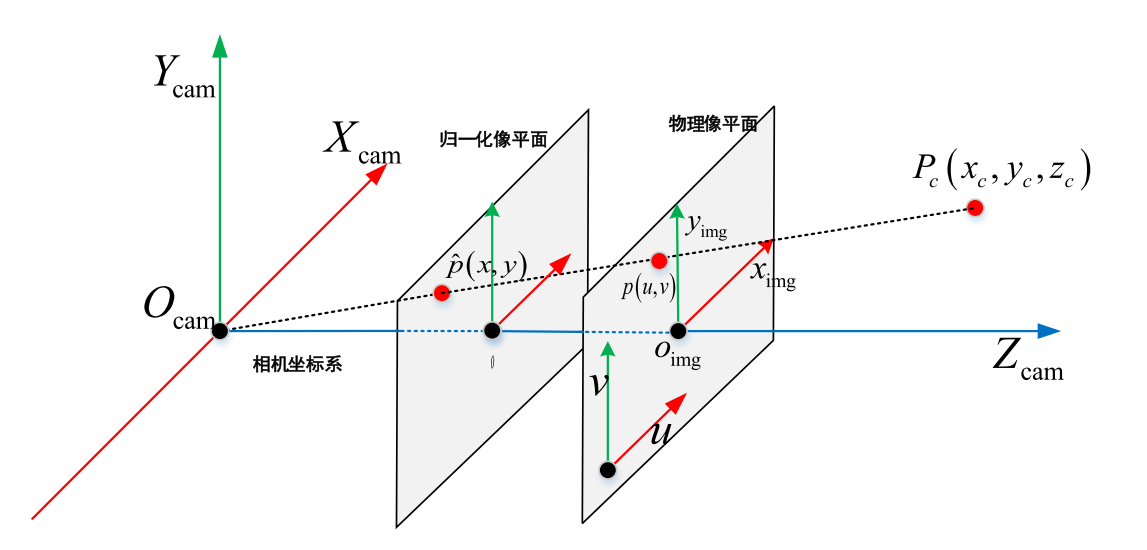
在投影的过程中,我们丢失了三维点的深度信息,通过小孔成像数学模型我们可以知道,通过单目相机我们理论上无法恢复图片中每一个点在原空间中的位置。在处理如三维重建等3D任务时,我们需要知道每一个点在原三维空间中的位置,这时只使用单目RGB相机难以达成我们的目标。
为了获取到三维信息,深度相机让我们能够在获取RGB图像的同时得到每一个像素点的深度值。深度相机一般有ToF(Time of Flight,时间飞行法)相机、结构光相机和双目相机。
ToF相机就是给目标发射连续的光脉冲,经过目标反射,通过传感器接受回来的光,记录飞行的时间,计算出到目标的距离。
结构光相机主要硬件有投射仪、相机,通过投射仪主动发射肉眼不可见IR红外光到被测物体表面,然后通过一个或多个相机拍摄被测物体采集结构光图像,将数据发送到计算单元,通过三角测量原理计算获取位置和深度信息。
而双目相机则是利用双目视觉来完成深度的测量,通过左右两个摄像头获取图像信息,计算视差,模拟人的双眼系统来获取深度信息。双目相机可以单纯依靠RGB拍摄的图片,也可以利用如透过DoE发射人眼不可见的pattern,通过接收器来得到图片进行双目立体匹配。
在此系列文章中,我们将会对双目视觉(Stereo Vision)深入了解。
双目相机的原理
双目相机实际上就是利用三角化的方式来定位两张图中对应pixel在3D空间的位置。
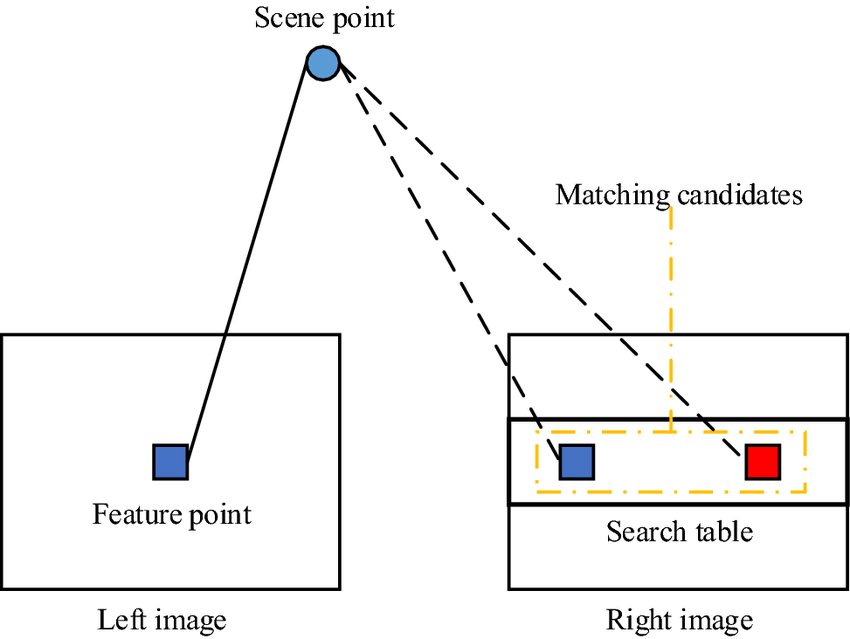
当我们有两张经过级线校正后(使两个相机位于同一水平线上)的左右相机图像时,对于左图的某个pixel,如果他没有在双目视觉系统中被遮挡,那么它能够在右图相同行找到与之对应的pixel,这个pixel就是3D空间中同一个点在左右相机拍摄到的点。那么通过相机内参、双目相机的baseline以及左图pixel需要移动N个pixel才能到达右图中对应点的位置(即视差)我们可以很容易算出左图(有图对应的)pixel它的深度值是多少。
所以在双目相机系统中,我们需要解决的问题就是给定的级线校正后的左图的点$p_l(x,y)$,它在级线方向在校正后右图对应点$p_r(u,v)$的位置是在哪。
双目立体匹配
从上一节的表述中我们可以知道,双目立体匹配是一项可以很简洁表述的任务,但仍然存在很多的难以解决的问题。
如拍摄的物体表面反光,在左右图片上反光区域不一致;左右相机存在光学不一致失真;低纹理区域难以匹配;重复出现的pattern以及遮挡区域无法匹配等问题,导致双目立体匹配仍然是一项具有挑战性的任务。
在传统的方法中,双目立体匹配一般包含以下步骤:
- 计算Cost
- Cost Aggregation
- 计算Disparity
- Refinement
稀疏匹配一般指提出左右图片的特征点后再做stereo matching的过程,而稠密匹配则是直接将整张图片通过局部或全局的方式进行匹配优化。
匹配代价
Absolute Difference
AD为绝对误差,如通过两个pixel的亮度或颜色的L1距离来代表两个pixel的匹配代价,公式如下:
$$
C_{AD}(p,d) = \sum |I_{left}(p)-I_{right}(p-d)|
$$
其中$p$代表左图中的点,$d$代表当前视差。
Sum of Absolute Difference
和AD相比,SAD多了一个局部窗口的概念,利用窗口中对应difference的信息来代表当前pixel的匹配代价,公式如下:
$$
C_{SAD}(p,d) = \sum_{p\in W_p} |I_{left}(p)-I_{right}(p-d)|
$$
其中$W_p$代表点$p$的邻域点。
Sum of Squared Difference
和SAD类似,但再SSD中采用了均方误差来代表匹配代价,更倾向于让其灰度信息更匹配,相比于SAD它对噪声更敏感。
$$
C_{SSD }(p,d) = \sum_{p\in W_p} |I_{left}(p)-I_{right}(p-d)|^2
$$
Normalized Cross Correlation
相比于对灰度值更敏感的SAD、SSD,NCC表征的是两个patch之间的相关性,如下公式所示。
$$
C_{NCC}(p,d) = \frac{\sum_{q\in W_p}|I_{left}(q) - I_{left}^{mean}(W_p)|\cdot |I_{right}(q) - I_{right}^{mean}(W_p)|}{\sqrt{\sum_{q\in W_p}|I_{left}(q) - I_{left}^{mean}(W_p)|^2\cdot \sum_{q\in W_p}|I_{right}(q) - I_{right}^{mean}(W_p)|^2}}
$$
其中$W_p$为基于点$p$的window区域,$I^{mean}(W_p)$代表这个window区域内的均值。
Census Transform
Census变换属于非参数图像变换的一种,它能够较好地检测出图像中的局部结构特征,如边缘、角点特征等。Census变换保留了窗口中像素的位置特征,并且对亮度偏差较为鲁棒,能够减少光照差异引起的误匹配。
Census变换的基本思想是:在图像区域定义一个矩形窗口,用这个矩形窗口遍历整幅图像。选取中心像素作为参考像素,将矩形窗口中每个像素的灰度值与参考像素的灰度值进行比较,灰度值小于或等于参考值的像素标记为0,大于参考值的像素标记为1,最后再将它们按位连接,得到变换后的结果,变换后的结果是由0和1组成的二进制码流。Census变换的实质是将图像像素的灰度值编码成二进制码流,以此来获取邻域像素灰度值相对于中心像素灰度值的大小关系。转换完成后,一般使用Hamming Distance来代表匹配代价。
Birchfield and Tomasi
BT方法主要解决图像深度不连续的问题,其目的是采样不敏感像素之间的相异性。标记$\overline{d}$为不匹配度,则有
$$
\overline{d}(p,d,I_{left},I_{right})=\min_{d-\frac{1}{2}\leq d_i \leq d+\frac{1}{2}}|I_{left}(p)-\hat{I}_{right}(p-d_i)|
$$
$[d-\frac{1}{2},d+\frac{1}{2}]$实际上就是对点的强度进行插值得到,即
$$
I^-(p)=\frac{1}{2}(I(p) + I(p-1))
$$
$$
I^+(p)=\frac{1}{2}(I(p) + I(p+1))
$$
然后有
$$
I^{min}(p)=\min{I^-(p), I^+(p),I(p)}
$$
$$
I^{max}(p)=\max{I^-(p), I^+(p),I(p)}
$$
因此,上述不匹配度可以转换为
$$
\overline{d}(p,d,I_{left},I_{right}) = \max{0, I_{left}(p)-I_{right}^{max}(p-d), I_{right}^{min}(p-d) - I_{left}(p)}
$$
Mutual Information
利用互信息来计算匹配代价是在SGM中提出,详见SGM。
后续
计算了匹配代价之后,经过不同的代价聚合等处理,我们能够得到一个$H\times W\times D$的prob volume,比如用Winner Take All的方式,找到每一个pixel中disparity维度最小的值作为这个pixel的disparity,或其它的一些算法,就能够计算出视差图。后续如经过双线性插值等方式对生成的Disparity进行refine得到一个更好的结果。