Implicit Geometric Regularization
IGR: Implicit Geometric Regularization for Learning Shapes
这篇发表于ICML 2020的文章介绍了一种对隐式表面表征的约束,从效果来看也是十分惊艳的,并且文章的方法也有说服力。

初读和困惑
输入为有向或无向点云(即是否带法向信息),训练MLP来判断Volume中每一个点的数值是多少。框架非常简洁明了,关键在于这个损失函数的构造。
$$
l(\theta)=l_{\chi}(\theta) + \lambda E_x(||\nabla_xf(x;\theta)||-1)^2
$$
上面的式子为文章提出的损失函数,其中$\lambda > 0$,是一个人为设置的超参数,$||\cdot||=||\cdot||_2$是欧几里德距离,第一项$l_\chi(\theta)$为
$$
l_\chi(\theta)=\frac{1}{|I|}\Sigma){i\in I}(f(x_i;\theta)+\tau||\nabla_xf(x_i;\theta)-n_i||)
$$
这一项的目的是为了当输入是有向点云即点云包含法向信息时,增加一个点$x$的发现约束。
而$\nabla$算子,文中表示它代表着程函方程,即
$$
||\nabla_xf(x)||=1
$$
一开始看到这就很懵了,程函方程不是电磁学的内容吗?咋用在这个损失函数里了?它代表啥意思?
再读与理解
我们抛开文中定义的程函方程,单看$\nabla\cdot$算子,他其实代表的也是梯度的计算,比如在Poisson重建中用到的解Poison方程也是用的$\nabla$算子。
那我们从梯度的角度来分析,程函方程这一个loss约束项本质上就是让表面附近的梯度为常数,即尽可能的让表面变化保持一致。
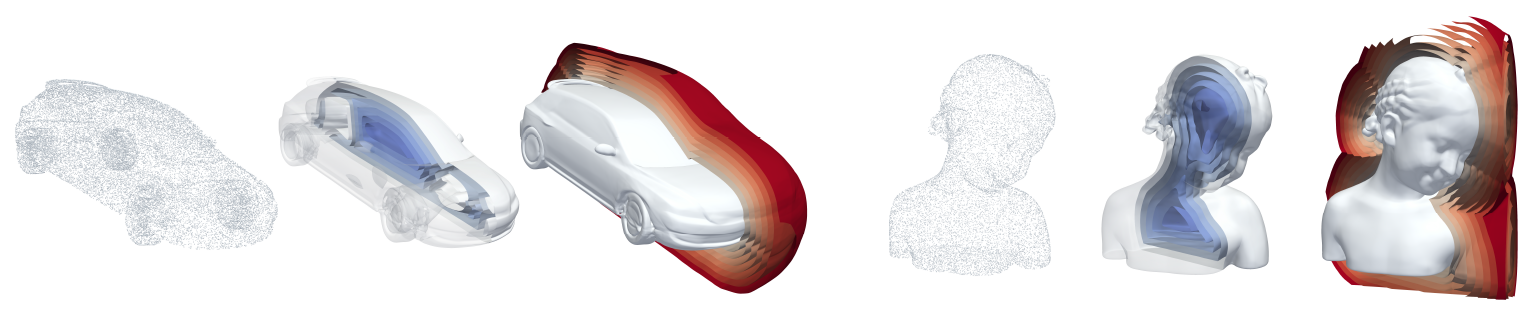
后续
之后文章证明了这个梯度方程也可以直接放在PyTorch中进行对应的计算和回传,因此可以很方便的将它嵌入到相应的任务中。
总体而言,IGR和Possion表面重建有异曲同工之处,利用曲面平滑约束来完成点云的曲面重建,并且IGR将其带入到了神经网络中来完成这项任务。
Shape As Points这篇文章则是用可微分的Poisson求解器来求解Poisson表面重建问题,后续有时间再详细介绍一下这篇工作。
IGR是一项优秀的工作,它易于嵌入并且在表征上有着合理的解释,在文章中也显示有很好的重建结果,是非常solid的工作。