图像的频域信息

最近在看一些文章的时候，采用了谱方法来解Poisson Equation，大部分采用的谱方法是用傅里叶变换来完成。同样在一些文章中将图片转换为频域信息进行分析，也是使用了傅里叶变换将空域图像转化为频域。因此稍微深入了解了一下二维图像的傅里叶变换。

在进入2D傅里叶变换前，我们先要回顾一下一维的傅里叶变换。

傅里叶变换

傅里叶变换，Fourier Transformation，是一种线性积分变换，常用于信号处理。它指的是一个一维的信号
可以被分解成若干个复指数波$e^{i\theta}$，而有欧拉公式$e^{i\theta}=\cos \theta + i\cdot \sin \theta$，因此每一个复指数波都是实部余弦波和虚部正弦波组成。

对于每一个正弦波（余弦波），都有频率、相位和振幅来决定，因此在频域中一维代表频率，每一个坐标对应的函数值是一个复数，复数的幅度代表振幅，相位角代表相位。

实际上一维傅里叶变换就是把一个复杂的波函数转化为一系列正弦余弦正交基的过程，如下图所示。

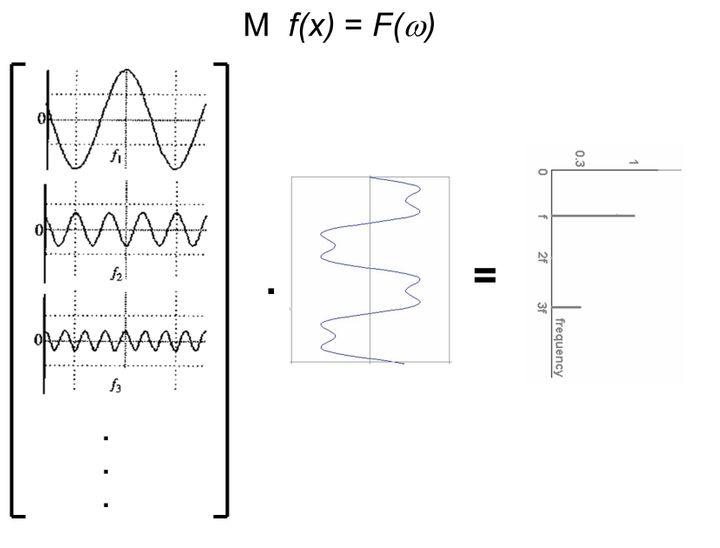
1D Fourier Transform

图像的傅里叶变换

那么在二维图片中，傅里叶变换实际上就是将一个图像分解成若干个复平面波$e^{j2\pi(ux+vy)}$之和，每一个复平面波就是二维变换的一个基函数。

二维傅里叶变换的公式如下：

$$
F(u,v) = \int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}f(x,y)e^{-j2\pi(ux+vy)}dxdy
$$

其中$F(u,v)$为变换后的值，$f(x,y)$为图像像素值，$u,v$为变换后图像的坐标，$x,y$为原图像的坐标，$j$表示复数。

但上述式子是在连续的空间中做的处理，我们在处理图像时实际上是处理的光栅化后的图片（即以像素为单位），因此我们真正使用的是二维离散傅里叶变换（2D Discrete Fourier Transform）。

我们以像素为单位进行采样，则有傅里叶变换
$$
F(u,v) = \Sigma_{x=0}^{M-1}\Sigma_{y=0}^{N-1}f(x,y)e^{-j2\pi(\frac{ux}{M}+\frac{vy}{N})}
$$

逆傅里叶变换：

$$
f(x,y) = \Sigma_{u=0}^{M-1}\Sigma_{v=0}^{N-1}F(u,v)e^{j2\pi(\frac{ux}{M}+\frac{vy}{N})}
$$

至此，我们可以用上述公式对图片进行傅里叶变换和逆傅里叶变换。另外需要注意的是，在这里我们输入的都是灰度图片。

二维DFT的python实现

DFT的实现如下:

@jit
def naive_DFT(image):
    assert len(image.shape) == 2
    H, W = image.shape
    # Prepare DFT coefficient
    G = np.zeros_like(image, dtype=np.complex128)
    
    # prepare processed index corresponding to original image positions
    x = np.tile(np.arange(W), (H, 1))
    y = np.arange(H).repeat(W).reshape(H, -1)
    

    # DFT
    for v in range(H):
        for u in range(W):
            G[v, u] = np.sum(image * np.exp(-2j * np.pi * (x * u / W + y * v / H))) / np.sqrt(H * W)

    # shift to recenter image
    shift_G = np.concatenate([G[H//2:,:], G[:H//2, :]], axis=0)
    shift_G = np.concatenate([shift_G[:,W//2:], shift_G[:, :W//2]], axis=1)
    return shift_G # show img using np.log(np.abs(shift_G))

iDFT的实现如下：

@jit
def naive_iDFT(fshift):
    assert len(fshift.shape) == 2
    H, W = fshift.shape

    # shift for inverse DFT caculation
    fshift = np.concatenate([fshift[(H+1)//2:,:], fshift[:(H+1)//2, :]], axis=0)
    fshift = np.concatenate([fshift[:,(W+1)//2:], fshift[:, :(W+1)//2]], axis=1)
    
    # Prepare iDFT coefficient
    G = np.zeros_like(fshift, dtype=np.float32)
    
    # prepare processed index corresponding to original image positions
    x = np.tile(np.arange(W), (H, 1))
    y = np.arange(H).repeat(W).reshape(H, -1)
    

    # iDFT
    for v in range(H):
        for u in range(W):
            G[v, u] = np.sum(fshift * np.exp(2j * np.pi * (x * u / W + y * v / H))) / np.sqrt(H * W)

    return np.abs(G)

同样，我们可以使用numpy中实现的FFT来完成相应的操作：

def numpy_FFT2(image):
    assert len(image.shape) == 2
    ft = np.fft.fft2(image)
    fshift = np.fft.fftshift(ft)
    return fshift # show img using np.log(np.abs(fshift))

def numpy_iFFT2(fshift):
    assert len(fshift.shape) == 2
    iffshift = np.fft.ifftshift(fshift)
    image = np.fft.ifft2(iffshift)
    return np.abs(image)