TSDF
TSDF
TSDF ,即Truncated Signed Distance Function,基于截断的带符号距离函数,是一种常见的在3D重建中计算隐势面的方法。TSDF是在SDF进行改进的,在拥有大内存的显卡并行计算的情况下,使用TSDF可以做到实时的重建效果,获得了很多方面的落地使用。
算法思想
TSDF的算法的思路就是用一个大的空间(Volume)作为要建立的三维模型,这个空间可以完全包括我们的模型,Volume由许多个小的体素(Voxel)组成。
每个Voxel对应空间中一个点,这个点我们用两个量来评价:
- 该Voxel到最近的Surface(一般称作Zero Crossing)的距离,记作TSDF(x),即带符号距离
- Voxel更新时的权重,记作w
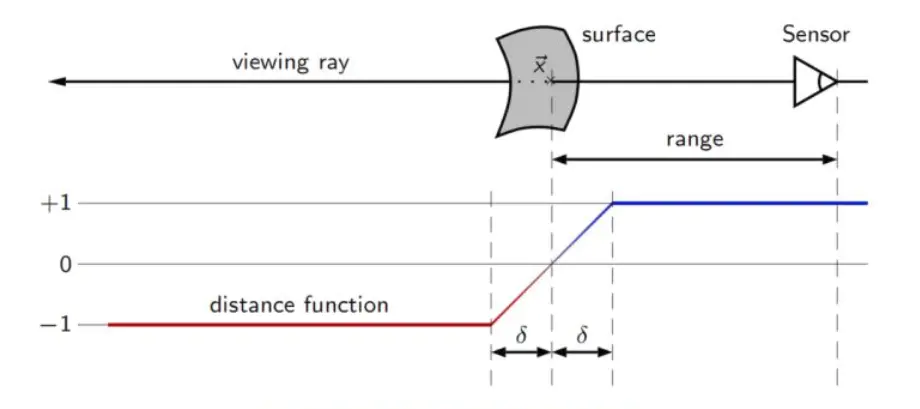
假设我们真实的面到相机的深度是ds,相机采集到的深度dv,那么符号距离值就是:
$d(x)=ds-dv$
当d(x)>0 时说明该体素在真实的面的前面,小于0 ,则说明该体素在真实的面的后面
每一次相机采集出来的数值,我们都认为是最大可能真实面,在相机前后也有可能是真实面,但是概率要小。这个前后距离我们对它进行一定的限制,因为离得特别远的话,其概率也是很小,我们就忽略了。
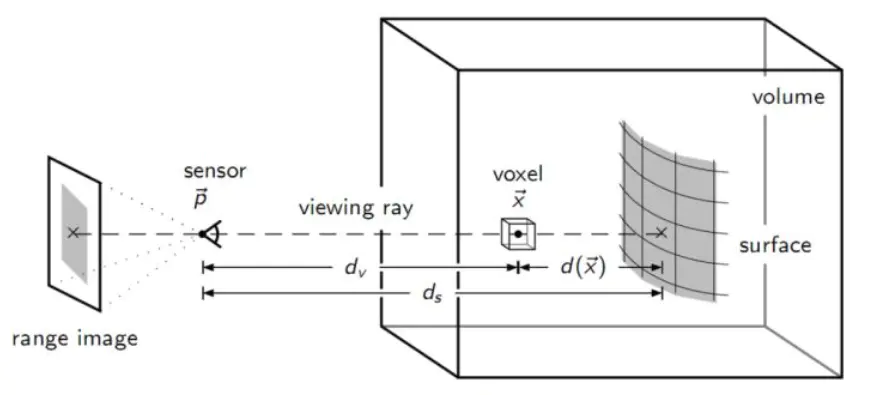
在计算新的拍摄帧的体素的符号距离值和体素更新的过程中,我们不是所有的体素都查找和更新,而是只查找更新截断距离内的体素,这也是TSDF与SDF不同的一点,大大缩短了计算量,并提高了精度
算法流程
准备工作
- 建立长方体包围盒,能够完全包围要重建的物体
- 划分网格体素,对包围盒划分n等分,体素的大小取决于包围盒和划分体素的数目决定。我们将整个空间的体素全部存入GPU运算,每个线程处理一条(x,y)。即对于(x,y,z)的晶格坐标,每个GPU进程扫描处理一个(x,y)坐标下的晶格柱
- 对于构造的立体中的每个体素g,转化g为世界坐标系下得三维位置点 p(根据体素的大小,以及体素的数目)
计算当前帧的TSDF值以及权重
这一步我们遍历所有的体素,以一个体素在世界坐标系三维位置点p为例
- 由深度数据的相机位姿矩阵,求世界坐标系下点p在相机坐标系下得映射点v,并由相机内参矩阵,反投影v点求深度图像中的对应像素点x,像素点x的深度值为value(x),点v到相机坐标原点的距离为distance(v)
- 位置点$p$的SDF值为$SDF(p)=value(x)-distance(v)$。现在我们就要引入截断距离了,计算出$TSDF(p)$, 公式写出来比较复杂,直接描述就是在截断距离$u$以内,$TSDF(p)=\frac{SDF(p)}{|u|}$, 否则,如果$SDF(p) >0$,$TSDF(p) = 1$;$SDF(p) <0$,$TSDF(p) = -1$
- 权重$w(p)$的计算公式:$w(p) = \frac{cos(\theta)}{distance(v)}$,其中θ为投影光线与表面法向量的夹角
经过我们这一步就算出这一帧的所有体素的TSDF值以及权重值
当前帧与全局融合结果进行融合
如果当前帧是第一帧,则第一帧即是融合结果,否则需要当前帧与之前的融合结果在进行融合。假设TSDF‘(p)为体素p的融合TSDF值,w’(p)为融合权重值,TSDF(p)为体素p当前帧的TSDF值,w(p)为当前帧权重值。现在我们要通过TSDF(p)更新TSDF’(p)。公式如下
$$
\begin{aligned}TSDF’(p)&=\frac{w’(p)\cdot TSDF’(P)+w(p)\cdot TSDF(p)}{w’(p)+w(p)}\w’(p)&=w’(p)+w(p)\end{aligned}
$$通过上述公式就可以将新的帧融合进融合帧内。
第一部分完成后,就是每添加一帧深度数据,执行一遍2、3步的计算,知道最后输出结果给Marching Cube计算提出三角面
算法特点
- 计算简单
- 需要大量并行计算加快速度
- 生成的网格的细节保持比较好,而且精确度也比较好,但是在边缘处以及前后景交界处,会出现较大的拖尾现象