Occypancy Networks

Occupancy Networks

Occupancy Networks: Learning 3D Reconstruction in Function Space

Target

将3D表面使用深度神经网络表示称连续的分类（二分类）问题。

核心思想

在空间体素中，需要重建的物体的占有率并不是离散的3D点位置，而是每一个可能的3D点$p\in \mathbb{R}^3$，均有推论函数（occupancy function）$o:\mathbb{R}^3 \to {0,1}$

利用神经网络估计推论函数，空间体素每一个点都能够预测一个0到1的占有率。实际上，网络就是进行一个二分类的判断，对于空间体素的每一个点都能够生成其是否为物体表面（是否在物体内部）的概率。

因此在使用网络进行重建之前，对于输入和输出进行了对应。对于给定的观测输入$x\in \mathcal X$，对于网络的输出$p\in \mathbb R^3$能够使用$(p,x)\in \mathbb R^3 \times \mathcal X$来表示。即对于一个参数化神经网络$f_\theta(\cdot)$，对于给定的pair $(p,x)$能够有

$$
f_\theta:\mathcal R^3 \times \mathbb X \to [0,1]
$$

其中，输入输出都为实数。

训练策略

在对象的三维边界体中随机采样点，对于第i个样本，采样K个点，然后评估这些位置的小批量损失为

$$
\mathcal L_\mathcal B(\theta)=\frac{1}{|\mathcal B|}\sum_{i=1}^{|\mathcal B|}\sum_{j=1}^K\mathcal L(f_\theta(p_{ij},x_i),o_{ij})
$$

$x_i$是batch B中的第i个观测值，$o_{ij}\equiv o(p_{ij})$，是点云的真实位置，$\mathcal L(\cdot,\cdot)$是交叉熵。

3D表征能够学习到概率隐变量模型，于是论文介绍了一个encoder网络$g_\psi(\cdot)$，使用位置$p_{ij}$和占有$o_{ij}$作为输入，最终预测出均值$\mu_\psi$和标准差$\sigma_\psi$，其满足高斯分布$q_\psi(z|(p_{ij},o_{ij}){j=1:K}$，且隐空间$z\in \mathbb R^L$。作者利用生成模型$p((o{ij}){j=1:K}|(p{ij})_{j=1:K})$负对数似然来优化下边界

$$
\mathcal L_\mathcal B^{gen}(\theta,\psi)=\frac{1}{|\mathcal B|}\sum_{i=1}^{|\mathcal B|}[\sum_{j=1}^K\mathcal L(f_\theta(p_{ij},z_i),o_{ij})+KL(q_\psi(z|(p_{ij},o_{ij})_{j=1:K})||p_0(z))]
$$

KL即KL散度，$p_0(z)$为隐变量$z_i$的先验分布，$z_i$是通过$q_\psi(z|(p_{ij},o_{ij})_{j=1:K})$采样得到。

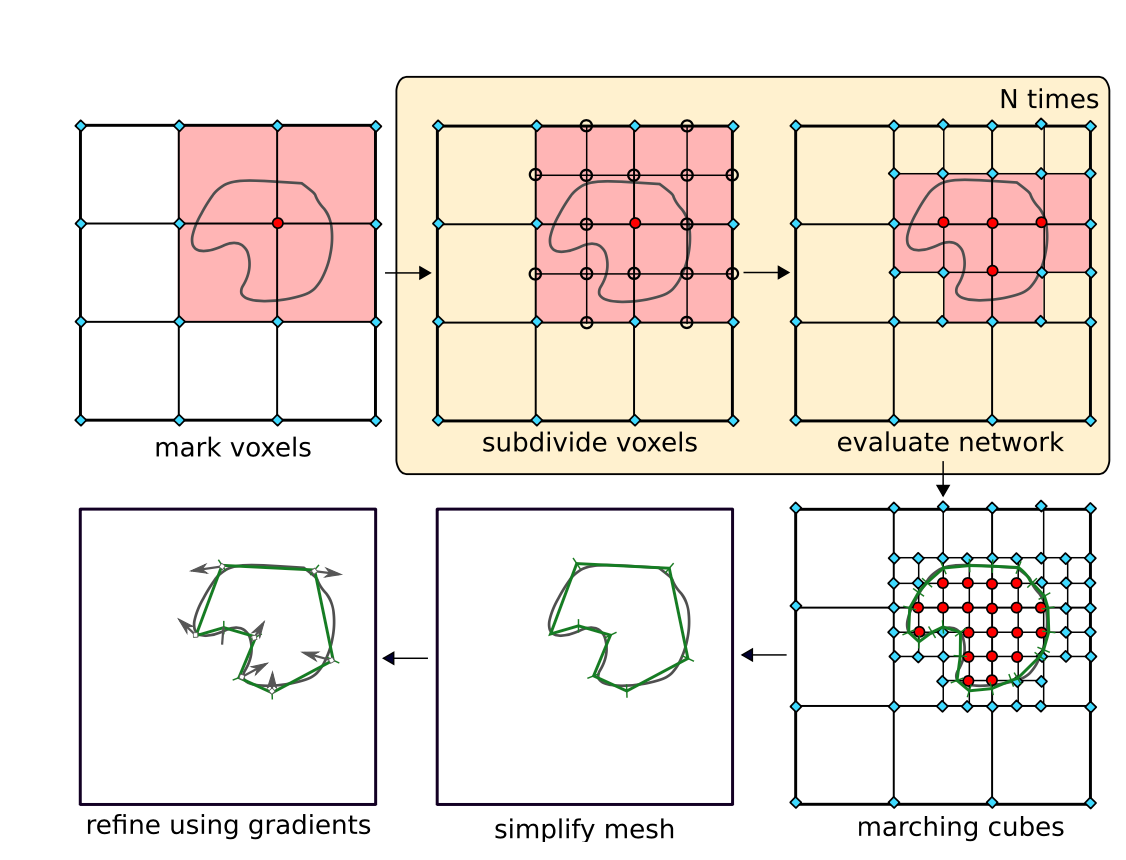
推理阶段

论文为了根据训练出的Occupancy Network在新的观测下得到的结果提取出等值面，提出MISE（Multiresolution IsoSurface Extraction，多分辨率等值面提取）。

首先在给定的分辨率上标记所有已经被评估为被占据（红）或未被占据（青）的点。然后确定所有的体素已经占领和未占领的角落，并标记（淡红），细分为4个亚体素。接下来，评估所有由细分引入的新网格点（空）。重复前两个步骤，直到达到所需的输出分辨率。最后使用Marching Cubes算法提取网格，利用一阶和二阶梯度信息对输出网格进行简化和细化。

实现细节

在论文给出的代码中，decoder部分最后一层为Conv1d而没有衔接Sigmoid/Softmax层，在loss函数计算的时候，使用BCE_with_logits来计算。同时，将输出的logits生成dist.Bernoulli分布，用KL散度与先验模型进行损失计算。

class DecoderCBatchNorm(nn.Module):
    ''' Decoder with conditional batch normalization (CBN) class.

    Args:
        dim (int): input dimension
        z_dim (int): dimension of latent code z
        c_dim (int): dimension of latent conditioned code c
        hidden_size (int): hidden size of Decoder network
        leaky (bool): whether to use leaky ReLUs
        legacy (bool): whether to use the legacy structure
    '''

    def __init__(self, dim=3, z_dim=128, c_dim=128,
                 hidden_size=256, leaky=False, legacy=False):
        super().__init__()
        self.z_dim = z_dim
        if not z_dim == 0:
            self.fc_z = nn.Linear(z_dim, hidden_size)

        self.fc_p = nn.Conv1d(dim, hidden_size, 1)
        self.block0 = CResnetBlockConv1d(c_dim, hidden_size, legacy=legacy)
        self.block1 = CResnetBlockConv1d(c_dim, hidden_size, legacy=legacy)
        self.block2 = CResnetBlockConv1d(c_dim, hidden_size, legacy=legacy)
        self.block3 = CResnetBlockConv1d(c_dim, hidden_size, legacy=legacy)
        self.block4 = CResnetBlockConv1d(c_dim, hidden_size, legacy=legacy)

        if not legacy:
            self.bn = CBatchNorm1d(c_dim, hidden_size)
        else:
            self.bn = CBatchNorm1d_legacy(c_dim, hidden_size)

        self.fc_out = nn.Conv1d(hidden_size, 1, 1)

        if not leaky:
            self.actvn = F.relu
        else:
            self.actvn = lambda x: F.leaky_relu(x, 0.2)

    def forward(self, p, z, c, **kwargs):
        p = p.transpose(1, 2)
        batch_size, D, T = p.size()
        net = self.fc_p(p)

        if self.z_dim != 0:
            net_z = self.fc_z(z).unsqueeze(2)
            net = net + net_z

        net = self.block0(net, c)
        net = self.block1(net, c)
        net = self.block2(net, c)
        net = self.block3(net, c)
        net = self.block4(net, c)

        out = self.fc_out(self.actvn(self.bn(net, c)))
        out = out.squeeze(1)

        return out

def compute_loss(self, data):
        ''' Computes the loss.

        Args:
            data (dict): data dictionary
        '''
        device = self.device
        p = data.get('points').to(device)
        occ = data.get('points.occ').to(device)
        inputs = data.get('inputs', torch.empty(p.size(0), 0)).to(device)

        kwargs = {}

        c = self.model.encode_inputs(inputs)
        q_z = self.model.infer_z(p, occ, c, **kwargs)
        z = q_z.rsample()

        # KL-divergence
        kl = dist.kl_divergence(q_z, self.model.p0_z).sum(dim=-1)
        loss = kl.mean()

        # General points
        logits = self.model.decode(p, z, c, **kwargs).logits
        loss_i = F.binary_cross_entropy_with_logits(
            logits, occ, reduction='none')
        loss = loss + loss_i.sum(-1).mean()

        return loss